前缀树

# 简介

我们想一下用百度搜索时候，打个 “一语”，搜索栏中会给出 “一语道破”，“一语成谶 (四声的 chen)” 等推荐文本，这种叫模糊匹配，也就是给出一个模糊的 query，希望给出一个相关推荐列表，很明显，hashmap 并不容易做到模糊匹配，而 Trie 可以实现基于前缀的模糊搜索。

注意这里的模糊搜索也仅仅是基于前缀的。比如还是上面的例子，搜索 “道破” 就不会匹配到 “一语道破”，而只能匹配 “道破 xx”

# 基本概念

假设一个场景：给你若干单词 words 和一系列关键词 keywords，让你判断 keywords 是否在 words 中存在，或者判断 keywords 中的单词是否有 words 中的单词的前缀。比 pre 就是 pres 的前缀之一。


朴素的想法是遍历 keywords，对于 keywords 中的每一项都遍历 words 列表判断二者是否相等，或者是否是其前缀。这种算法的时间复杂度是 $O(m * n)$，其中 m 为 words 的平均长度，n 为 keywords 的平均长度。那么是否有可能对其进行优化呢？答案就是本文要讲的前缀树。


我们可以将 words 存储到一个树上，这棵树叫做前缀树。 一个前缀树大概是这个样子：

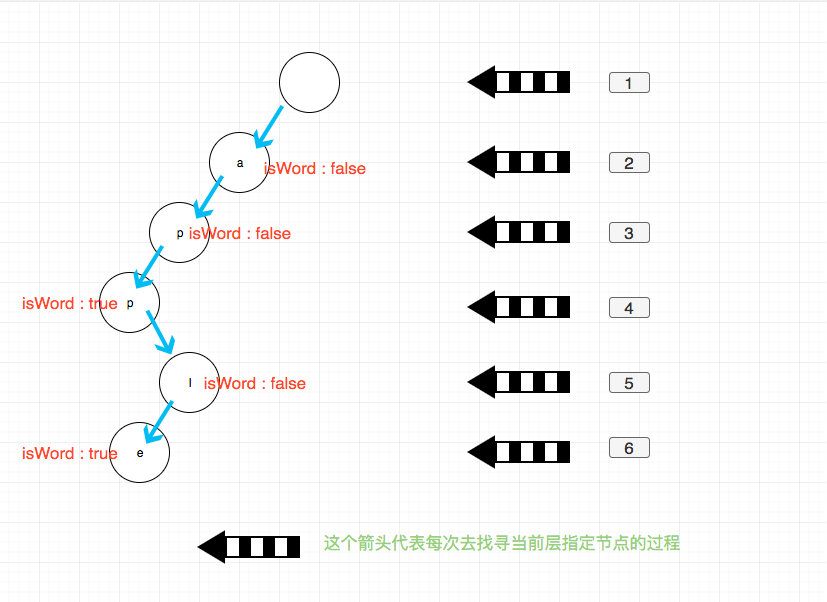
如图每一个节点存储一个字符，然后外加一个控制信息表示是否是单词结尾，实际使用过程可能会有细微差别，不过变化不大。


为了搞明白前缀树是如何优化暴力算法的。我们需要了解一下前缀树的基本概念和操作。

# 节点

• 根结点无实际意义
• 每一个节点数据域存储一个字符
• 每个节点中的控制域可以自定义，如 isWord (是否是单词)，count (该前缀出现的次数) 等，需实际问题实际分析需要什么。
  一个可能的前缀树节点结构：

private class TrieNode {

        int count; // 表示以该处节点构成的串的个数

        int preCount; // 表示以该处节点构成的前缀的字串的个数

        TrieNode[] children;

        TrieNode() {

            children = new TrieNode[26];

            count = 0;

            preCount = 0;

        }

    }

# Trie 的插入

构建 Trie 的核心就是插入。而插入指的就是将单词（words）全部依次插入到前缀树中。假定给出几个单词 words [she,he,her,good,god] 构造出一个 Trie 如下图：

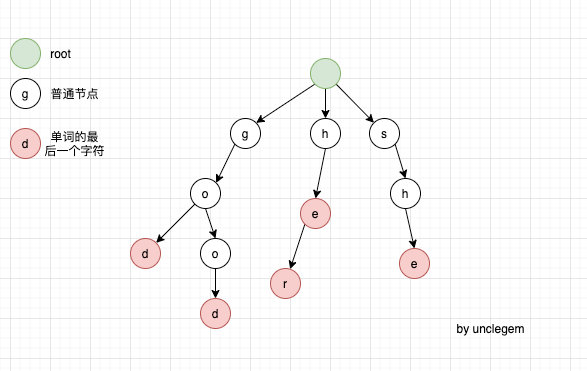
也就是说从根结点出发到某一粉色节点所经过的字符组成的单词，在单词列表中出现过，当然我们也可以给树的每个节点加个 count 属性，代表根结点到该节点所构成的字符串前缀出现的次数

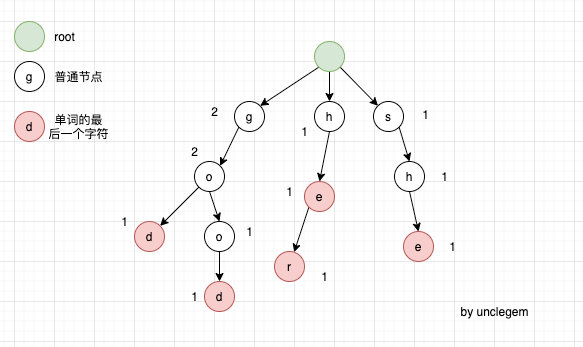
可以看出树的构造非常简单：插入新单词的时候就从根结点出发一个字符一个字符插入，有对应的字符节点就更新对应的属性，没有就创建一个！

Trie 插入的代码讲解，首先 root 是空节点，index 用来判断从哪条路开始，得到走哪条路之后，判断是否为空，为空就创建一个节点（相当于开辟了一条路），然后把节点指向更新到下一个节点，进行循环操作

# Trie 的查询

查询更简单了，给定一个 Trie 和一个单词，和插入的过程类似，一个字符一个字符找

• 若中途有个字符没有对应节点 →Trie 不含该单词
• 若字符串遍历完了，都有对应节点，但最后一个字符对应的节点并不是粉色的，也就不是一个单词 →Trie 不含该单词

# Trie 模版

// 前缀树的模板代码

public class TrieNode {

    public int pass;

    public int end;

    public TrieNode[] nexts;

    public TrieNode() {

        pass = 0;

        end = 0;

        nexts = new TrieNode[26];

    }

    public static class Trie {

        private TrieNode root;

        public Trie() {

            root = new TrieNode();

        }

        public void insert(String word) {

            if (word == null) {

                return;

            }

            char[] chars = word.toCharArray();

            TrieNode node = root;

            int index = 0;

            for (int i = 0; i < chars.length; i++) {

                index = chars[i] - 'a';

                if (node.nexts[index] == null) {

                    node.nexts[index] = new TrieNode();

                }

                node = node.nexts[index];

                node.pass++;

            }

            node.end++;

        }

        public int search(String word){

            if (word==null){

                return 0;

            }

            char[] chars = word.toCharArray();

            TrieNode node = root;

            int index = 0;

            for (int i = 0; i < chars.length; i++) {

                index = chars[i]-'a';

                if (node.nexts[index] == null){

                    return 0;

                }

                node = node.nexts[index];

            }

            return node.end;

        }

    }

}

# 复杂度分析

• 插入和查询的时间复杂度自然是$O(len(key))$，key 是待插入 (查找) 的字串，即时间复杂度为查询的结果的深度
• 建树的最坏空间复杂度是$O(m^{n})$, m 是字符集中字符个数，n 是字符串长度，以 26 个英语字母为例，建树三层，为 26 的三次方，因为每个节点最大都能分出 26 条路

# 前缀树的特点

简单来说， 前缀树就是一个树。前缀树一般是将一系列的单词记录到树上， 如果这些单词没有公共前缀，则和直接用数组存没有任何区别。而如果有公共前缀， 则公共前缀仅会被存储一次。可以想象，如果一系列单词的公共前缀很多， 则会有效减少空间消耗。

而前缀树的意义实际上是空间换时间，这和哈希表，动态规划等的初衷是一样的。

其原理也很简单，正如我前面所言，其公共前缀仅会被存储一次，因此如果我想在一堆单词中找某个单词或者某个前缀是否出现，我无需进行完整遍历，而是遍历前缀树即可。本质上，使用前缀树和不使用前缀树减少的时间就是公共前缀的数目。也就是说，一堆单词没有公共前缀，使用前缀树没有任何意义。

# 总结

前缀树的核心思想是用空间换时间，利用字符串的公共前缀来降低查询的时间开销。因此如果题目中公共前缀比较多，就可以考虑使用前缀树来优化。

前缀树的基本操作就是插入和查询，其中查询可以完整查询，也可以前缀查询，其中基于前缀查询才是前缀树的灵魂，也是其名字的来源。

基于前缀树的题目变化通常不大， 使用模板就可以解决。如何知道该使用前缀树优化是一个难点，不过大家只要牢牢记一点即可，那就是算法的复杂度瓶颈在字符串查找，并且字符串有很多公共前缀，就可以用前缀树优化。