# 基础
- 栈和队列的相互转换:队列进去的顺序是 1 --> 2,1 --> 3,2,1,队列进去的顺序是 1,2,3
- 数组长度 api 没有小括号,s.length; 即可
- 递归三要素 (二叉树问题基本都是递归,然后通过递归三部曲解决问题)
- 确认递归函数的参数和返回值:确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数,并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型
- 确认终止条件:写完了递归算法,运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出
- 确认单层递归的逻辑:确认每一层递归需要处理的信息。在这里也就是重复调用自己来实现递归过程
- Queue<> queue = new LinkedList<>() 队列,底层用链表实现
- offer () 增加节点,如果超过容量会返回 false,不会抛出异常
- add () 增加节点,只不过如果超过容量会抛出异常提醒
- remove () 删除节点,如果不存在,会抛出异常
- poll () 删除节点
- element()
- peek () 如果队列不为空,返回这个队列队头的元素,但不删除。如果队列为空,第一个方法抛出 NoSuchElementException,第二个返回 null
- isEmpty () 是否为空
- Queue<> queue = new ArrayDeque<>() 队列,底层用循环数组实现
- Deque<> queue = new LinkedList<>() 双端队列,底层用链表实现
- addFirst()
- addLast()
- offerFirst()
- offerLast () 将给定的对象添加到双端队列的队头或者队尾,如果这个双端队列已满,前面两个方法将抛出 IllegalStateException,而后面两个方法返回 false
- removeFirst()
- removeLast()
- pollFirst()
- pollLast()
- getFirst()
- getLast()
- peekFirst()
- peekLast()
# 二叉树
-
![下标]()
-
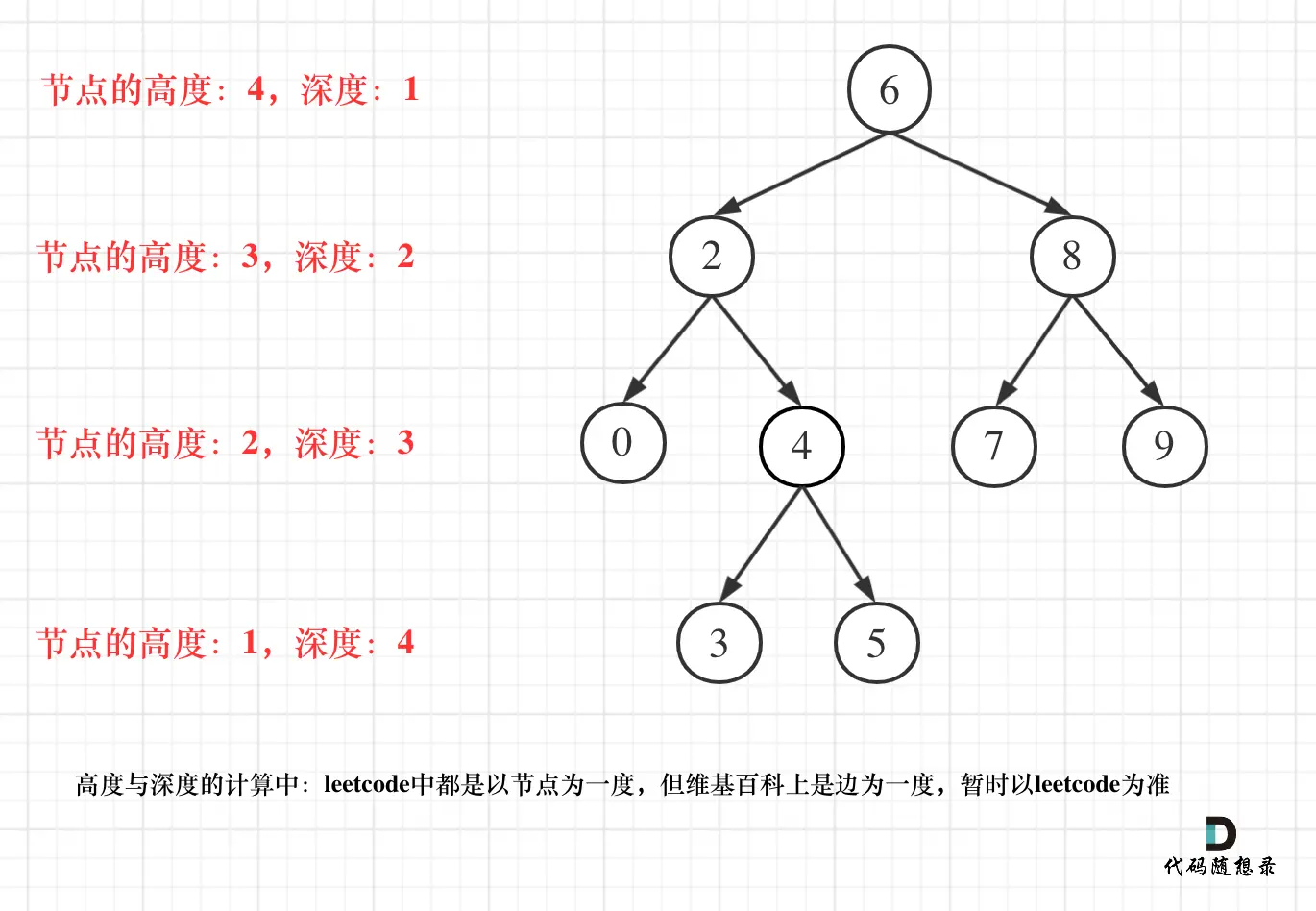
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
![二叉树深度高度]()
-
数组到集合 Arrays.asList ()
-
集合到数组 coll.toArray ()
-
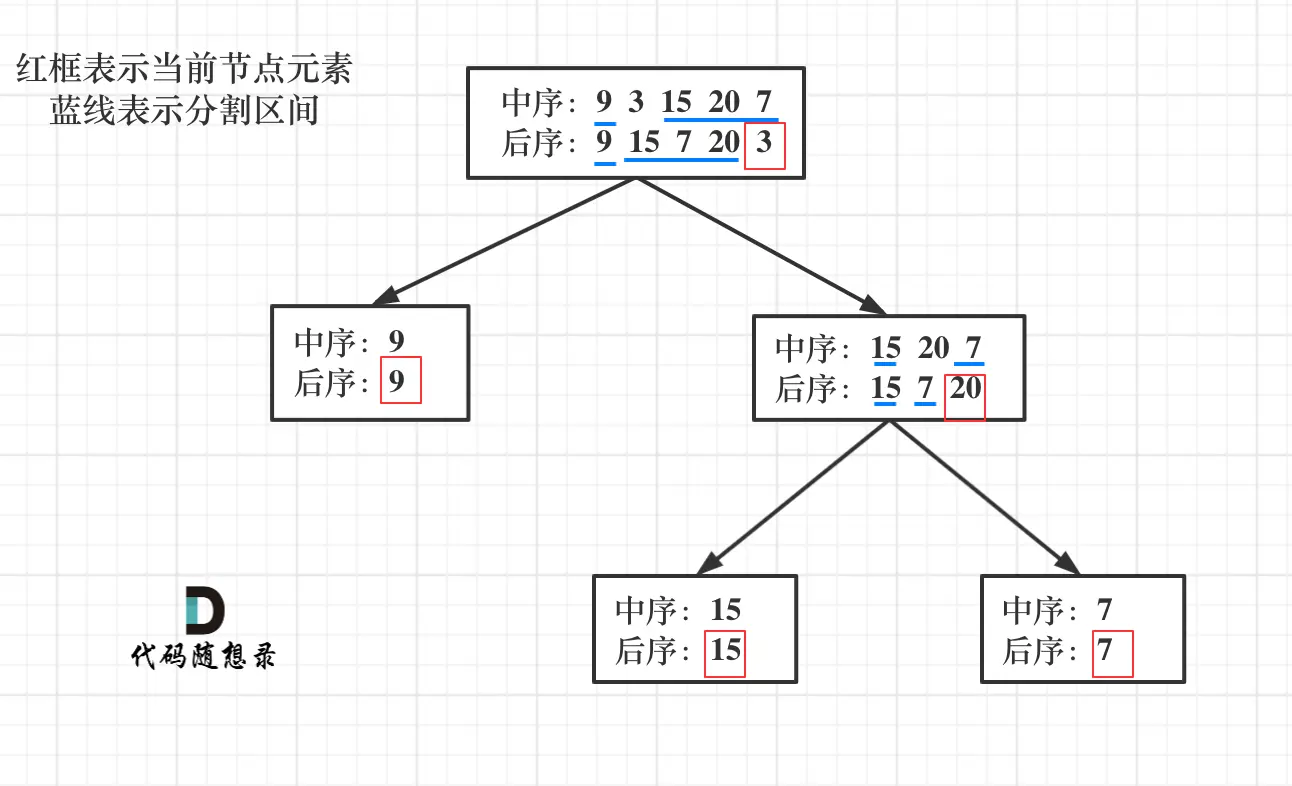
如何根据两个顺序构造一个唯一的二叉树,以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
流程图:
![生成二叉树]()
-
在递归遍历的时候,什么时候直接 return 递归函数的返回值,什么时候不用加这个 return 呢?如果要搜索一条边,递归函数就要加返回值,这里也是一样的道理。因为搜索到目标节点了,就要立即 return 了,这样才是找到节点就返回(搜索某一条边),如果不加 return,就是遍历整棵树了。
-
二叉树中通过递归的时候返回 TreeNode 节点可以来增加 删除节点
-
在二叉树题目选择什么遍历顺序:
- 涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
- 求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算
- 求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
# 回溯
- 回溯算法模板
void backtracking(参数) { | |
if (终止条件) { | |
存放结果; | |
return; | |
} | |
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { | |
处理节点; | |
backtracking(路径,选择列表); // 递归 | |
回溯,撤销处理结果 | |
} | |
} |
- 回溯递归中关于组合问题:对于组合问题,什么时候需要 startIndex 呢?
我举过例子,如果是一个集合来求组合的话,就需要 startIndex,例如:77. 组合 (opens new window),216. 组合总和 III (opens new window)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用 startIndex,例如:17. 电话号码的字母组
-
回溯算法中 backtrack (candidates,target,sum+candidates [i],i+1); 让 sum 当参数传出去,可以减少对 sum 的回溯
-
回溯模板非常重要,回溯算法解决都是套用回溯模板 yyds
# 动态规划
- 状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定 dp 数组(dp table)以及下标的含义
- 确定递推公式
- dp 数组如何初始化
- 确定遍历顺序
- 举例推导 dp 数组
动态规划中状态转移方程里下标为 i 的行只参考下标为 i - 1 的行的话,就可以优化空间,即定义长度为固定长度的 temp,可以把 dp 数组空间从 O (n) 优化到 O (1)